Inferring mRNA from Protein

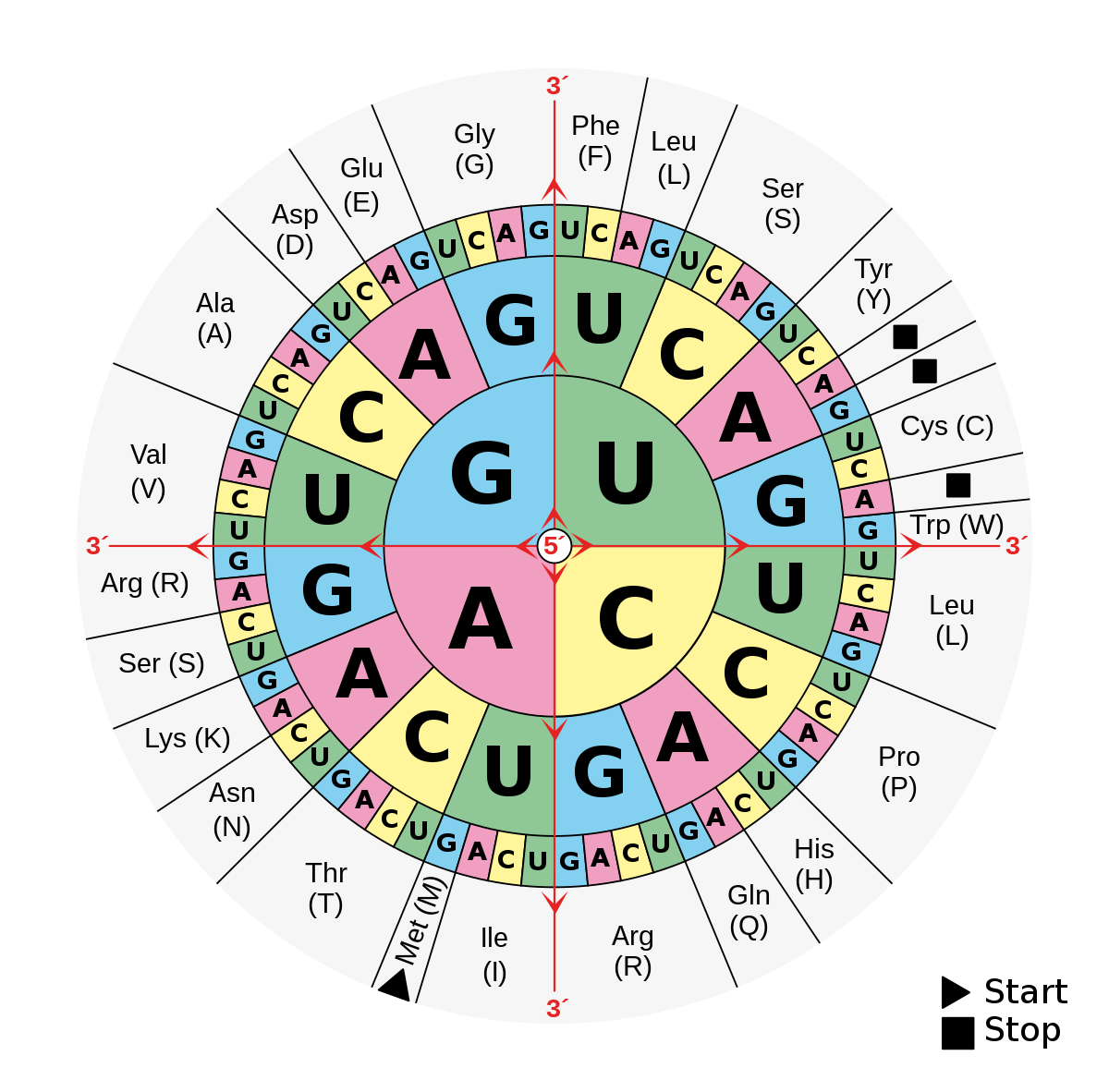
The standard RNA codon table organized in a wheel, from Wikipedia.

This problem asks:

Given: A protein string of length at most 1000 aa.

Return: The total number of different RNA strings from which the protein could have been translated, modulo 1,000,000.

Restate the problem

First, if you’re not familiar with it, the modulo operator is described well here and here.

They’re going to send me a protein string that might be as long as a thousand amino acids. In the “Translating RNA into Protein” challenge, I got the RNA string and used the RNA codon table to calculate the resulting protein string. This challenge asks for a similar calculation going in the opposite direction. Given the protein string, how many different RNA strings could possibly have coded for the given string.

Solution steps

First, I copied the RNA codon table out of the problem statement as a Python set because I wanted to be able to iterate over all the possible encodings.

Then, I built a second Python set of all the different frequencies of the different codons. This set answers the question, “For each protein, how many different ways are there for RNA to encode this protein?”

Next, I built the codon frequencies set by counting the number of times each protein appeared in the codon table as shown below:

def codon_frequencies():
    frequencies = {}
    for k, v in RNA_CODON_TABLE.items():
        # print(k, v)
        if not v in frequencies:
            frequencies[v] = 0
        frequencies[v] += 1
    # print (frequencies)
    return frequencies

Then, for every protein in the downloaded dataset, I look the protein up in my codon frequencies table and multiply the existing count of encodings by the number of different ways to encode that protein.

This number gets extremely large very quickly, so I did a

mod 1000000

after every protein. The full code is here.

Making the codon_frequencies set and iterating through the proteins, multiplying each time, was the only way I could think to do this.

Python concepts

Sets are the only new Python tool used in this challenge. It’s helpful to understand the four built-in collection types for Python: lists, tuples, sets, and dictionaries.

Mathmatics concepts

In addition to introducing modular arithmetic, this challenge required the use of multiplying probabilities when calculating the probability that multiple independent events will ALL occur. If this isn’t clear, it’s probably worth investigating in depth now, because future challenges will rely on knowing how to calculate probabilities for independent events.